 al
calculations
al
calculationsSundi al
calculations
al
calculations
Left image: a traditional Islamic sundial (photo © Germán Moreno, 2006). The shadow has just reached the outer curved vertical, indicating time for Islamic afternoon prayers. The image on the right is the Tower of Voices portion of the planned Flight 93 Memorial. It is also an Islamic sundial. Shadow calculations confirm that, on any day of the year, when the Tower shadow reaches the inner arc of trees, it will be time for Islamic afternoon prayers.
This comparison graphic, together with the above caption, was run as ad copy in a number of western Pennsylvania newspapers a couple of weeks before the July 28, 2007 public meeting of the Flight 93 Memorial Project. If your visit to this site was prompted by this ad, thanks for having eyes to see. It is amazing how many people do not.
While the overt likeness between a traditional Islamic sundial and the Tower of Voices can be seen just by looking, the shadow calculations necessary to confirm that the Tower of voices is in fact an Islamic sundial are quite tedious. In contrast, other Islamic and terrorist-memorializing features, like the Mecca orientation of the giant crescent, are trivially easy to confirm. Those looking for the simplest proofs of the worst features should begin with either the Proof of Betrayal page, or with the Crescent of Betrayal poster (a high resolution map of the site plan with critical information superimposed).
If anyone actually wants to check the shadow calculations for the tower-sundial, my original calculations were posted on my Error Theory blog in October 2005. The presentation is cleaned up a bit in my Crescent of Betrayal book, where Chapter 4 (in download 2) provides the basic analysis. Detailed calculations appear in Addenda Seven and Eight, which for convenience are reproduced below.
Important update: Memorial Project Chairman John Reynolds dismisses my sundial analysis on grounds that prove he has never even looked at it! (Muslim prayer times are determined by shadow length, while Reynolds' argument assumes they are determined by shadow angle.)
Plus a new discovery: Murdoch's preliminary design also contained a year-round accurate Islamic prayer-time sundial!
Unlike the tricky sundial in the final design that switches gnomon height sometime in mid-November, the sundial in the preliminary design is a simple traditional Islamic sundial. It is on the same epic scale as the sundial in the final design. Both are built around a similar height Tower of Voices (specified at 93 feet in the final design and seeming to be about the same in the original design). But where the final design looks at first glance to be slightly inaccurate between mid-November and late-January, the original is immediately seen to give the proper time for Islamic afternoon prayers throughout the entire year (assuming a 93 foot Tower height).
The original sundial was also in a completely different location from the final one, so nobody can say this is not a completely different sundial. A single year-round accurate Islamic prayer-time sundial could never occur by accident. Two of them? Double never.
Addendum Seven: Shadow calculations and other esoterica from the Tower-sundial
Here is my graph of where the tower's shadow falls at the beginning of the time for Islamic afternoon prayers. As the year progresses from June to December, the shadow hits further and further up the magenta prayer-line, then starts moving back down.
To understand the zig zag in the prayer line, you have to read Chapter 4. This is not the place to start trying to understand the Tower sundial!
To put together my shadow calculations, I took advantage of a number of very helpful online resources. Most important is J. Giesen’s Sun Shadow Applet.[1] Giesen’s applet the length and direction of the shadow cast by any gnomon, at any time of the day, at any point on the earth. Just set the applet to 40.03 north latitude and 78.54 West longitude, set GMT to -5, turn off Daylight Savings Time, and set the gnomon height to 28.35 meters (93 feet), which is height of the Tower at the bottom of its crescent shaped top (the highest point of solid shadow, whether or not the slot is in play). Since the bottom of the crescent coincides with the slotted southwest side of the tower, it is this side of the tower that serves as the origin from which shadow length and angle are projected.
Giesen’s applet can be used to calculate Islamic afternoon prayer times (asr prayers). For any day, use the applet to find the shortest shadow of the day (somewhere near noon). Add this length to 28.35 meters, and look for the time in the afternoon when the Tower’s shadow reaches this length. That is the asr prayer time. Simpler is just to go to one of the Islamic websites that hosts an Islamic prayer time calculator. I used the one at qibla.org. Just plug in the latitude and longitude of the crash site, set GMT to -5, turn Daylight Savings Time off, and the calculator will generate daily prayer times by month and year.
With prayer time for a given day in hand, plug this time and date into Giesen’s applet and it will tell you the length of the shadow and the angle of the shadow. It gives the angle by giving the Sun’s azimuth in degrees clockwise from north. Subtract 180 from this to get the angle of the shadow clockwise from north. If your graphics program enables polar coordinates, you can plot these lengths and angles directly onto a screen shot of the Tower array. (On a Windows PC, pressing “Alt” and “Print Screen” will copy a screen shot of your active browser window to you clipboard, allowing you to paste it into other programs. To take a screen shot of your entire screen, omit the “Alt”.)
If you are using Microsoft Paint you will need to do what I did and convert your polar coordinates (angle and length) into Cartesian coordinates. For this, I used the online coordinate converter provided by Kusashi.com.[2] This calculator assumes that angles are measured counter-clockwise from east, so you will have to subtract your degrees clockwise from north from 90 before using it. Plug this angle into the “argument” box, plug shadow length into the modulus box and press calculate. The real component of the result will be your x coordinate and the imaginary component of the result will be your y coordinate (both in meters, since that was what you inputted in the modulus).
These meters then need to be converted to pixels, according to the number of pixels to the meter in the screen-shot you are using. When I take a screen shot of Murdoch’s Tower Plan PDF zoomed to 900%, a pixel count of the scale shows 4.74 pixels to the meter. (If you want to download the original PDF and verify this for yourself, the PDF is now behind password protection in the Park Service archives You can get a password by calling 814 443-4557.) Thus I multiply my meter measurements by 4.74 to plot them on my Tower Plan graphic. It is a little cumbersome, but pretty simple once you get everything set up.
Here is the bit of screen shot on which I graphed my results. (Click on image to bring up the original.)
And here are my shadow calculations, (slightly different from the calculations in my original sundial post because I discovered that I had entered the latitude wrong for my original calculations, 40.3 degrees north instead of 40.03 degrees north):
June 16th 2005 (longest day of the year)
Asr = 4:15 PM; (modulus, argument) = (37.39, -.6); (x, y) in meters = (37.39,
-.39); (x, y) in pixels = (177, -2).
The critical point is the bottom of the gnomon, which as I constructed it has Cartesian coordinates of (x,y) = (164, 426). (Coordinates are counted down to the right, starting from the origin at the upper left. I chose this point by inscribing the crescent shaped cross-section of the Tower with a circle and projecting a line through the center of the circle that follows the angle of the Tower platform (rise 100, run 70). Where this line cuts the bottom of the circle is the gnomon point. (The color versions use (163, 426) as their origin point. (164, 426) looks more accurate, so I switched to this for the B+W.)
Adding the June 16th run and rise of (177, -2)
to the (41, 324) gnomon location puts the end of the June 16th asr
prayer-shadow at (341, 428). [Note that Paint counts pixels from the upper left
corner of the graphic, so it reads (Δx, Δy) of (177, -2) as (177, 2).]
July 16th 2005
Asr = 4:19 PM; (modulus, argument) = (38.71, 1.8); (x, y) in meters = (38.70,
1.22); (x, y) in pixels = (183, 6), which is very close to the line for June,
and just a few pixels longer. The changes become more rapid as the sun gets
lower. Upper point at (347, 420). The Asr connecting line ending at this point
starts at (341, 428) and travels (Δx, Δy) = (6, -8). [Paint reads (Δx, Δy) = (6,
-8) as (Δx, Δy) = (7, -9) because it counts from one instead of zero. You can’t
draw a line zero px. long in Paint.]
August 16th 2005
Asr = 4:08 PM; (mod, arg) = (43.12, 10.9); (x, y meters) = (42.42, 8.17); (x, y
pixels) = (201, 39). Upper point at (365, 387). The Asr connecting line ending
at this point starts at (347, 420) and travels (Δx, Δy) = (18, -33).
September 16th 2005
Asr = 3:40 PM; (mod, arg) = (51.86, 24.2); (x, y meters) = (47.30, 21.26); (x, y
pixels) = (224, 101). Upper point at (388, 325). The Asr connecting line ending
at this point starts at (365, 387) and travels (Δx, Δy) = (23, -62).
October 16th 2005
Asr = 3:06 PM; (mod, arg) = (62.1, 37.9); (x, y meters) = (49.00, 38.15); (x, y
pixels) = (232, 181). Upper point at (396, 245). The Asr connecting line ending
at this point starts at (388, 325) and travels (Δx, Δy) = (8, -80).
November 16th 2005
For November and December, there are two shadow ends to calculate, one taking
the bottom of the top crescent to be the top of the tower and one taking the
bottom of the upper slot to be the top of the tower:
Shadow cast from full tower height:
Asr = 2:38 PM; (mod, arg) = (76.63, 49.8); (x, y meters) = (49.46, 58.53); (x, y
pixels) = (234, 277). Upper point at (398, 149). The Asr connecting line ending
at this point starts at (396, 245) and travels (Δx, Δy) = (2, -96).
Shadow from bottom of upper slot:
82% of (234, 277) is (192, 227). Lands at (356, 199).
December 16th 2005 (not plotted)
Shadow cast from full tower height:
Asr = 2.34 PM; (mod, arg) = (87.15 , 55.4); (x, y meters) = (49.49, 71.74); (x,
y pixels) = (235, 340). Upper point at (399, 86).
Shadow from bottom of upper slot:
82% of (235, 340) is (193, 279). Lands at (357, 147).
December 21st 2005 (shortest day of the year)
Full tower height:
Asr = 2.36 PM; (mod, arg) = (86.32 , 55.5); (x, y meters) = (48.89, 71.14); (x,
y pixels) = (232, 337). Upper point at (396, 89). The Asr connecting line
ending at this point starts at (398, 149) and travels (Δx, Δy) = (-2, -60).
[Microsoft Paint does not plot this line segment correctly, so in my graphic I
just placed a vertical line starting 1 pixels left of the previous Asr line
segment.]
Shadow from bottom of upper slot:
82% of (232, 337) is (190, 276). Lands at (355, 237). The Asr connecting line
ending at this point starts at (356, 199) and travels (Δx, Δy) = (-2, -49).
Dividing date between tall and short gnomon heights:
A line along the Tower shadow in Murdoch’s Tower Plan detail has a slope of 194 pixels of rise for every 191 px. of run. That is a little less than 45 degrees down from north, 44.55 degrees from N to be exact.
On November 3rd 2005, asr prayers occur at 2:47 PM, when the sun’s azimuth is 224.5 degrees from N, projecting its shadow to 44.5 degrees from north, almost exactly the angle depicted in Murdoch’s graphic. Since light is reaching the ground through the slot at this angle (as can be seen from the graphic), that means that the lower gnomon height, created by the bottom of the slot, is what determines prayer time on November 3rd.
It appears from the graphic that the light through the slot is about to get closed off as the sun continues westward. Note that the crescent edge, visible at the tip of the Tower shadow, is lined up the thin shaft of light making it through the slot. Any more westward movement of the sun and this crescent edge will block light through the slot from reaching the ground. Since prayers occur later at earlier dates, this means that light through the slot probably does not reach the ground at prayer time just a couple of days earlier. The exact date cannot be determined from the graphic so I used November 1st as a best guess.
To plot the transition, it is necessary to calculate both the tall and short prayer-time shadows for this date.
November 1st 2005
Full tower height:
Asr = 2.49 PM; (mod, arg) = (69.23 , 44.7); (x, y meters) = (49.21, 48.70); (x,
y pixels) = (233, 231).
Shadow from bottom of upper slot:
82% of (233, 231) is (191, 189).
Starting from the Tower Detail gnomon position of (x, y) = (163, 426), these tall and short shadow-falls land at (397, 195) and (355, 237) respectively. These points demark the zig and the zag in the prayer-shadow-line, which then connects the dots to the other shadow end points. The zig zag segments are plotted as follows:
From the Oct. 16th Asr shadow to the upper point of the zig, start at (396, 245) and travel (Δx, Δy) = (1, -50).
The zig line starts at (397, 195) and travels (Δx, Δy) = (-42, 42).
From the bottom of the zag to the Nov. 16th Asr shadow for the short gnomon height, start at (355, 237) and travel (Δx, Δy) = (1, -38).
Fer de Vries computer program
Sundial expert Fer de Vries developed a computer program for calculating Islamic prayer lines for any specified gnomon at any specified latitude. I sent him an early version of my connect the dots derivation of the Tower’s asr-prayer-line and he sent it back with his computer generated lines for the specified gnomon height and the Shanksville latitude superimposed:
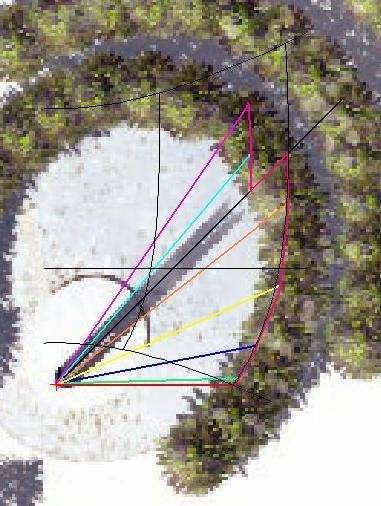
Fer de Vries’ asr prayer-line matches mine almost exactly. The validity of the results still depend on the validity of my assumption that the Tower base is at the same level as the trees, and Fer's program does not address the validity of the zig zag in the asr line, but his program does confirm that my calculations for the main asr line are reasonably accurate. [3]
The migrating gnomon
For those who want to be completely thorough, note that once light through the slot gets closed off by the westward movement of the sun, the point that casts the bottom of the top of the Tower’s shadow will start to move up the westward arm of the Tower’s crescent shaped top. The sunlight that comes over the bottom of the crescent shaped top will, like any sunlight through the slot, get blocked from reaching the ground by the eastern wall of the tower. The two arms of the crescent will create a shadow with a pointed bottom (one side vertical, one side curved out and up) that gets shallower in shape as the sun sets.
Technically, the gnomon migrates clockwise around the tower, starting at the slot and moving around to about due west. This will have very little effect on where the bottom of the top of the Tower’s shadow lands at asr-prayer time. Initially, the gnomon point comes around to the west (away from the ellipse of trees) more than it rises. That will pull the asr-prayer line inwards a bit in late October, where it is out towards the outer side of the ellipse of trees, but it will not affect the tip of the zig.
Once the sun reaches due west (where it is at June asr prayer times) the gnomon point will have climbed by about .4 of the radius of the tower. (If the Tower top were sliced at a 45 degree angle and it was pointed north, then the western side of the tower would be the taller than the slot side by the radius of the Tower. As it is, the tower top is sliced at a 30 degree angle, according to the Tower Section view, yielding 2/3s of the height gain of a 45 degree slice. Also, the tower-crescent points 35 degrees clockwise from north. That cuts the rise down by roughly 35/90 = 39 percent, and 61 percent of 2/3s = .41.) At 35 degrees from north, the slot-gnomon is positioned .57r west of the center of the Tower circle (sine or cosine of 35, depending on where you are measuring your degrees from). The due-west gnomon (the June gnomon), is r west of center, so it moves west (away from the ellipse of trees) by about the same amount that it rises: about .4r. Lastly, June asr prayer shadows descend at an angle substantially flatter than 45 degrees (their length of 37.39 meters, compared to the Tower height of 28.35 meters, implies an angle of descent of 36.22 degrees). With the June gnomon rising about the same amount as it moves away from the tree line, this flatter than 45 degree shadow path to earth will push the Tower’s asr-prayer time out by a modest fraction of the radius of the tower. Since the prayer-line at that point is a bit towards the inside of the tree line, this moves it a little closer to the base of the trees.
[3] Fer de Vrie’s website has a link to his computer program: http://www.dse.nl/~zonnewijzer/haf-hal.htm.
Addendum 8: Discrepancies between different site-plan views in the tower-sundial analysis
Shadow calculations are sensitive to any change in assumptions about the topography of the ground where the shadows are landing, or about the exact dimensions of the shadow-caster. The calculations above require a couple of assumptions, but they both seem to be well justified.
The first assumption is that the bottom of the Tower is at the same level as the inner ellipse of trees (i.e. that the ground is flat). Is this assumption correct? The site-plans include a Tower Section detail that shows the Tower sitting on a raised base, about ten feet above grade. It also depicts the trees in the background as planted at grade-level, below the raised base. If this section view is correct then my assumptions about the topography are incorrect. Instead of sitting at the same level as the trees, the Tower sits ten feet above, and its shadows fall correspondingly further out.

Tower Section view from the Tower of Voices PDF page, shows base of tower well above the grade where the trees are planted behind. If this is accurate, the tower is a good ten feet higher than I was assuming, and its prayer-time shadows will fall out beyond the inner arc of trees. [Med rez image. More rez available in PDF.]
As it turns out, the Tower Section view misrepresents the topography of the site. Terraserver’s topo map of the area shows that in the fifty meters from the Tower to the tree line, the grade slopes up about ten feet: just enough to bring the trees up to the bottom of the base of the Tower. The map also shows a topo line running pretty much along the path of the asr prayer line, meaning that the line of trees is itself level (not sloping up to the left as depicted in the Tower Section view).

Terraserver’s topo map of Tower of Voices site. The Tower is located just about at the last zero in 2400. There is twenty feet of elevation change between contour lines, and the inner arc of trees is about half-way to the next higher contour line to the right, making for an elevation gain at the tree line of about ten feet.[1]
Is Murdoch’s Tower Section detail intentionally misleading? Having done the shadow calculations himself, Murdoch would know that there are sundial societies like NASS (the North American Sundial Society) with experts on Islamic sundials who could recognize his sundial in a minute if he didn’t disguise it.[2] I sent my shadow calculations to Islamic-sundial expert Fer de Vries, who quickly verified my asr line. (See Addendum 6 for Fer’s calculations.) Thus it makes sense that Murdoch might want to misrepresent the topography of the site so as to throw off the shadow calculations of anyone who tried to investigate. What we can say for certain is that, intentionally or not, the Tower Section view is misleading.
Sundial Assumption Two: The Depth of the Slot
A second assumption in my calculations is that the slot depth indicated by the shadow in the Tower Plan drawing (18 percent of the Tower height) is accurate. This information is contradicted, however, by the depth of the slot depicted in the Tower Section view (above). Here the slot is claimed to be very short, only 8 percent of the Tower height. So which is the real plan? Short slot or long slot?
A third view is also available, the view up the tower, seen in Figure 40 above. This view depicts the slot coming well down into the field of wind-chimes. Contrast this with the Tower Section view, where the slot is depicted as coming down only to very slightly below the top of the topmost wind chime. It is hard to tell exactly how deep the slot is cut in the up-the-tower view, but it is definitely a lot more than 8 percent (or one-twelfth) of the way.
That makes it two views against one, and the view that indicates the shorter slot has already been proven to contain misinformation about the topography of the Tower site, giving another reason to favor the information in the other two views.
Perhaps most importantly, note that the plan-view, which shows the slot at 18% of the height of the Tower, is a CAD projection from a 3D model. You can tell that by the shadows cast by the trees. A computer calculated the shadows, implying that a computer also calculated the Tower shadow, based on a 3D model of the Tower. The existence of such a 3D model is pretty strong evidence that this is the real design. At the least, there is a lot more work involved in creating a 3D model of the slot, and what we can certainly say is that at least ONE of Murdoch's specifications creates a year round accurate Islamic prayer-time sundial.
The Mecca Orientation
Finding the Islamic sundial adds meaning to the Mecca orientation of the Tower crescents. When time for afternoon prayers arrives, the Muslim faithful will need some way to determine the direction to Mecca, and Murdoch has provided it. All they have to do is walk out towards the mouth of the inner ellipse of trees, sight down the line of upper crescent tips, and they will be looking towards Mecca:
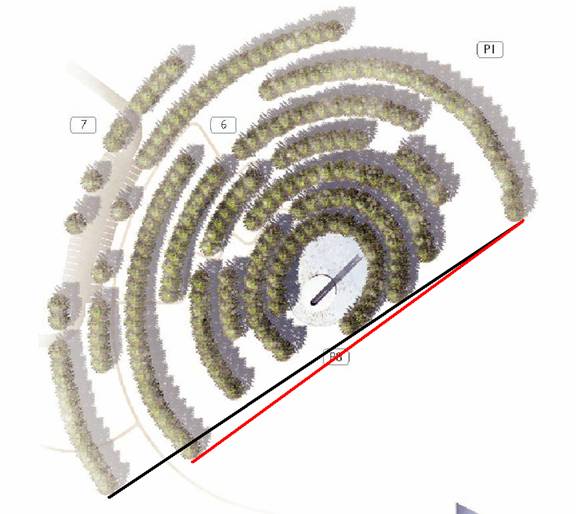
Tower detail with crescent-tip lines. When these lines were drawn onto the Tower portion of the Crescent site-plan (figure 32 in chapter 4) the black line pointed directly at Mecca. You can see here that this black line is the sight line, along the tips of the Tower crescents in the northeast direction, affording a person coming out from the Tower-sundial a visual reference for Mecca.
Interestingly, this detail graphic of the Tower array seems to be rotated clockwise a small amount vis a vis the lower resolution site-plan graphic of the Tower array seen earlier. In the site-plan image, the line across the most obtruding crescent tips (red) points 1.8° north of Mecca, and the line to the further away and more recessed crescent tip (black) points exactly at Mecca. Here the red line points about 1.4° north of Mecca and the black line points about 1° south of Mecca.
I don’t know what accounts for these small discrepancies between the different Tower views. My guess would be that Murdoch decided (finally) to exercise a modicum of caution, as he seems to have done with his misleading Tower Section view. There is no reason he had to include the full Islamofascist precision of his design in the publicly available plans at all. He could have fudged many details and only put the exact plan into the engineering drawings.
What is really surprising is how much he did reveal. The most likely explanation is pride. Why depict the shaft of light passing through the slot in the tower at just the time of day when a little further westward movement of the sun will close this shaft off, changing the effective gnomon height of the tower? If he hadn’t done that, I could not have figured out the zig-zag in his asr prayer line. But Murdoch had to include this key information. After all, if the Crescent of Embrace did not win (and what are the chances that the jury would pick a giant red crescent for the memorial to Flight 93?), the submitted plans would be all anyone would ever see of Murdoch’s brilliant creation. He couldn’t leave out the key elements that made the design a work of genius.
Those who are looking for any possible excuse not to see the Islamic and jihadist elements of Murdoch’s design might take the lack of exact consistency in the different views of the crescents of trees that surround the Tower of Voices as evidence that the Mecca orientations of these crescents is coincidental. That is about as much of a reed as the deniers have to hang on: that only one of the two available images of the Tower crescents shows them to be turned exactly 90° from the central crescent, while the other shows them turned almost exactly 90°. Maybe a person who focuses hard enough on that small discrepancy can even avoid seeing the year-round-accurate Islamic prayer-time sundial Towering overhead.
[1] From TerraServer’s topo map of Shanksville PA, 7/1/1977 (http://terraserver.microsoft.com/). There are also some contour lines, without altitude numbers, in the Crescent site plan. Examination of figure 24 back in chapter 3 reveals a contour line running pretty much exactly along the inner arc of trees.
[2] NASS has a website at http://sundials.org/.
Free download of Crescent of Betrayal, the Director's Cut.
Order print edition of Crescent of Betrayal.
Crescent of Betrayal, main page
John Reynolds' interview with Brian Whipkey and Vicki Rock of the Somerset Daily American
All content of this website © Alec Rawls 2007